Introduction

La suite de la saga sur la notion d’apprentissage artificiel (que l’on désigne également par apprentissage automatique) appliquée aux tâches de classification et regroupement.

• Apprentissage artificiel
• Fondements et protocoles pour la classification et les regroupements
• Moyens d’apprendre pour la classification et les regroupements (biais et modèles)
• Évaluation de l’apprentissage – Estimation des risques
• Évaluation de l’apprentissage – Précision / Rappel / F-mesure

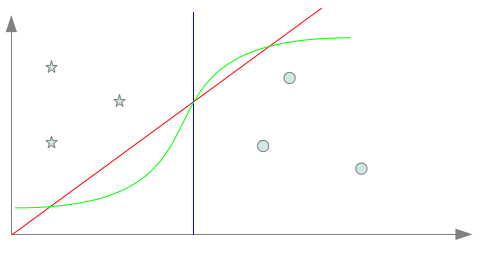
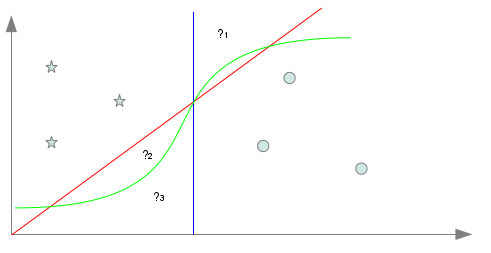
Dans ce volet, nous allons introduire les notions complémentaires de biais et modèles d’apprentissage.

Moyens d’apprendre : de la nécessité du biais d’apprentissage…

Dans le billet précédent, nous avons vu que les algorithmes d’apprentissage artificiel avait pour but de s’adapter à la résolution d’une tâche au travers d’un protocole d’apprentissage. Bien que nous ayons vu les différents protocoles pertinents pour nos tâches de classification et regroupement (non supervisés et supervisés), nous n’avons pas discuté des moyens employés par ces derniers pour parvenir à cette adaptation. C’est là le but principal de ce deuxième billet.

Pour bien comprendre les enjeux des moyens à employer pour l’apprentissage, nous devons partir de la problématique concrète. Nous allons prendre un exemple sur la classification : supposons que nous devions apprendre à classer deux types de documents caractérisés par deux attributs et que nous disposons de trois exemples de chaque (ce cas n’est pas réaliste en terme d’apprentissage mais nous permet d’illustrer simplement nos propos). La localisation dans l’espace d’entrée des six exemples est alors donnée par le graphique suivant :

Afin d’apprendre à distinguer les deux types de documents, nous devons concrètement apprendre à les séparer, c’est à dire déterminer un séparateur. Dans le cas donné ci-dessus, il est possible de déterminer une multitude de séparateurs différents tout à fait acceptables au vu des données présentées. Les séparateurs bleu, rouge et vert sur le diagramme ci-dessous en sont trois exemples.

=> Lequel de ces séparateurs est meilleur que les autres?
=> Y en a t-il d’ailleurs un meilleur?

Les trois séparateurs présentées ici sont tout à fait convenables et valides mais celui en rouge est certainement le plus simple : il s’agit d’une combinaison linéaire sur les deux attributs. Cependant, cette question n’est pas dénuée d’intérêts car si ici nous n’avons présenté volontairement que des séparateurs “acceptables” nous verrons dans un prochain volet que cela n’est pas forcément toujours le cas…

Mais revenons pour l’heure à nos différents séparateurs. S’ils sont tous les trois acceptables (et il y en a sûrement d’autres), il va pourtant falloir choisir l’un d’entre eux. Si nous voulons faire le choix de la simplicité, nous pouvons nous contenter d’un séparateur linéaire mais rien ne nous oblige à faire ce choix. En d’autres termes, nous allons devoir ici arbitrer des caractéristiques du séparateur que nous désirons utiliser.
=> Choix 1 : Le séparateur doit être simple : être une combinaison linéaire des attributs
=> Choix 2 : Le séparateur doit être complexe : être une fonction polynomiale sur les attributs

Derrière ces réflexions se cache en réalité un problème bien connu et fondamental de l’apprentissage qu’est celui de l’induction. Nous disposons dans notre exemple de 6 points différents étiquetés dans les deux catégories. Si choisir un séparateur qui distingue correctement les 6 points selon les deux catégories est une chose, nous ne devons pas perdre de vue que notre objectif est de classer n’importe quel point de l’espace selon les deux catégories. Cela implique d’obtenir une règle de classification valable idéalement pour tout point de l’espace à partir seulement de quelques exemples… C’est là l’induction nécessaire à tout apprentissage. Prenons trois points inconnus notés ?1, ?2 et ?3 dans l’exemple précédent. Il est évident que selon le séparateur retenu parmi les trois proposés, la classification des trois points ne sera pas la même. Cela montre l’importance des choix inductifs faits sur la classification des points inconnus et donc plus généralement sur la tâche visée.

Faire un choix inductif, c’est choisir un biais inductif servant de biais d’apprentissage. Il s’agit de manière générale de fixer des conditions / hypothèses que doit respecter le système apprenant pour apprendre la tâche. Ces conditions ont l’objectif essentiel de limiter les hypothèses faites par le système apprenant sur ce qu’il doit apprendre. Utiliser un “bon” biais est vital pour l’apprentissage en deux points :

• L’efficacité de l’apprentissage : si les hypothèses envisageables par l’apprenant sont restreintes, l’apprentissage sera alors plus efficace. Concrètement, s’il y a moins d’hypothèses à considérer, on va plus vite à trouver la meilleure. A l’inverse, s’il y en a de trop l’algorithme risque de ne jamais converger vers une solution.
• La pertinence de l’apprentissage : si le biais est bien choisi, les hypothèses envisageables par l’apprenant correspondront à la réalité de la tâche. Cela améliorera grandement la pertinence de l’apprentissage. Concrètement, dans l’exemple précédent si ?1 doit normalement être classé en tant qu’étoile, le séparateur bleu n’est pas pertinent.

Un bon apprentissage passe bien sûr par un biais respectant au maximum ces deux points. A l’inverse la violation de ces points par le biais va avoir pour conséquence une dégradation forte de l’apprentissage. Nous aurons l’occasion de voir des exemples de “mauvais” biais et de situations de mauvais apprentissage lors d’un prochain billet.

… à la notion de modèles d’apprentissage

Un point clé de l’apprentissage artificiel est la notion de modèle.

Le modèle va permettre à l’apprenant d’apprendre efficacement selon un biais et de restituer cette connaissance en accomplissant la tâche désirée. Le choix du modèle à employer est donc primordial pour réussir un apprentissage optimal. Concrètement, le choix d’un modèle non adapté à la tâche aboutira à coup sûr à un mauvais apprentissage. Le choix du modèle est donc corrélé à la notion de biais défini précédemment dans le sens où le modèle impose toujours un type de biais sur l’apprentissage.

Ce biais est d’une nature différente selon le modèle retenu :

• fonctionnel : il est alors basé sur une fonction de décision sur les attributs d’entrées permettant d’établir une séparatrice. La plus célèbre et la plus simple est sans doute la fonction linéaire mais il en existe de plus complexes couramment utilisées comme les fonctions polynomiales ou sigmoïdes. On entend assez souvent parler de régression dans le sens où l’on réduit le problème à une fonction dont on fixe les paramètres en fonction du problème.
• probabiliste : il est alors basé sur une distribution de probabilité sur les attributs des entrées. Concrètement, cela revient à établir un modèle qui en fonction des données qu’on lui présente donne la probabilité de chaque étiquetage. Les réseaux bayésiens sont sans doute l’exemple typique de ce genre de modèle.
• connexionniste : il est alors basé sur un réseau de neurones. Ce type de modèle s’inspire à la base du fonctionnement du cerveau humain. La tâche est découpée en neurones spécialisées dans la reconnaissance d’une partie de celle-ci. Lorsqu’un neurone spécifique est activé (on parle de stimulus), la partie de la tâche associée est reconnue. Nous citerons les perceptrons ou encore les cartes de Kohonen comme exemples typiques connexionnistes.
• temporelle : il est alors basé sur un couplage temporelle entre les entrées. Ce type de modèle décrit différents états temporels dans lesquels on est susceptible de se trouver (et par lesquels on va transiter). On peut alors déduire la tâche de l’état courant. L’exemple typique est le modèle de Markov caché.

Perspectives

Dans le prochain billet, nous abordons l’évaluation de l’apprentissage.

Mots clefs : apprentissage artificiel, biais d'apprentissage, biais inductif, classification, clustering, induction, modèles d'apprentissage, moyens de l'apprentissage, séparateur linéaire, TAL

Cette entrée a été publiée le Mercredi 25 juillet 2012 à 12 h 02 min, et rangée dans Apprentissages, TAL. Vous pouvez suivre les réponses à cette entrée via son flux RSS 2.0. Vous pouvez laisser un commentaire, ou faire un rétrolien depuis votre site.