Blog Onyme
Grammaires formelles et analyse syntaxique des langues27 octobre 2010IntroductionDans ce billet, nous allons expliciter les notions relatives à l’analyse syntaxique des langues et les grammaires formelles. Au commencement était la grammaire…Ce terme de “grammaire” doit vous être familier mais de quoi s’agit il exactement? Un truc casse pieds que l’on apprend à l’école primaire? Eh bien pas seulement. A l’école primaire, on nous apprend que la grammaire, c’est l’ensemble des règles qu’il faut appliquer pour écrire un français correct. Cette définition ne se rapporte en fait qu’à la grammaire de la langue française. Nous allons donc voir ici une généralisation de ce concept que l’on appelle la théorie des grammaires formelles. Définition formelleUne grammaire dans un sens formel se compose de quatre éléments :
Vous êtes perdus? Pas de panique, Nous allons voir ce que cela donne avec la grammaire française. Exemple avec la grammaire française
Prenons un exemple avec une pseudo grammaire française : S -> VN Dans cette exemple minimaliste, les non terminaux sont constitués par les concepts de verbe (V), nom (N), déterminant (D), sujet (SU), noyau verbal (VN) ainsi que par l’axiome S de notre grammaire. Les terminaux sont quant à eux, les mots le, un, chat, lion, mange et sort. Chaque ligne représente une règle de production différente où le non terminal de la partie gauche peut être obtenu en combinant les terminaux / non terminaux de la partie droite. Ainsi, un nom peut être obtenu par le terminal “chat” ou bien par le terminal “lion” (5ème règle). De même, un noyau verbal peut être obtenu en combinant successivement un sujet et un verbe (2ème règle). Enfin, l’axiome de la grammaire peut être obtenu en réalisant un noyau verbal (1ère règle). Il faut comprendre par là que toute phrase correcte pour cette pseudo grammaire est constituée d’un noyau verbal. Exemple avec une grammaire formelle et notion de dérivationVoici un autre exemple de grammaire, non rattaché à la langue cette fois : S -> Ab Où S est le non terminal jouant le rôle d’axiome, A et B des non terminaux et a et b les terminaux. De manière générale, une grammaire permet de générer un langage (le langage français dans le cadre de la grammaire française). On dit alors que le langage est accepté, reconnu par la grammaire. Un langage se caractérise par l’ensemble des dérivations de la grammaire l’ayant engendré. Les dérivations sont des séquences de symboles terminaux de la grammaire de telle manière que l’application successive des règles de la grammaire depuis l’axiome permette d’aboutir à cette séquence de terminaux. Une dérivation est parfois aussi appelée un mot du langage (mais ne correspond pas avec la notion de mots dans la langue française). Pour notre grammaire d’exemple, le mot (dans le sens des grammaires formelles) bbab est une dérivation de la grammaire car une application successive des règles de notre grammaire permet d’obtenir cette séquence de terminaux à partir de l’axiome. 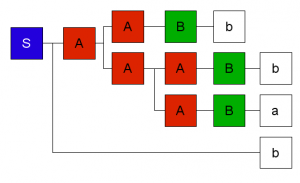 Par contre, le mot aba n’est pas une dérivation de cette grammaire et n’appartient donc pas au langage généré par cette dernière car le dernier symbole terminal de la séquence ‘a‘ ne peut être obtenu en appliquant les règles successives. 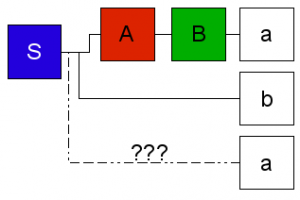 De manière formelle, l’ensemble des mots dérivés de cette grammaire peut être représenté par l’expression régulière “[ab]+b“. Cela en fait une grammaire de type régulière comme nous l’explicitons par la suite. Pour notre pseudo grammaire française, le mot “le chat sort” est une dérivation tandis que le mot “le chat dort” n’en est pas une. 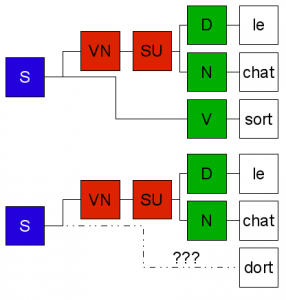 5 types de grammaires : la hiérarchie de ChomskyDans ses travaux, Chomsky distingue 5 types de grammaires (dont 4 sont en fait couramment utilisés dans l’état de l’art) dans ce qu’il appelle la hiérarchie de Chomsky :
 On parle de hiérarchie car tous les langages / grammaires d’un niveau x dans la hiérarchie sont également inclus dans les niveaux y de la hiérarchie où y<x (forme de pyramide comme l’illustre le schéma ci dessus). Ainsi, les grammaires non contextuelles sont aussi contextuelles (avec un contexte nul) et récursivement énumérables (si un mot appartient à un langage généré par une grammaire, on peut le déterminer en un temps fini) mais pas nécessairement régulières (dont les dérivations sont descriptibles par une expression régulière). A chaque type de grammaire / langage correspond des méthodes d'analyses particulières (valables donc aussi pour les niveaux plus élevés de la hiérarchie) … puis vint l’analyse syntaxiqueL’analyse syntaxique est le procédé visant à établir un arbre de dérivation entre une grammaire et une séquence de terminaux donnée (une dérivation si l’analyse est un succès). En d’autre terme, il s’agit de déterminer si la séquence est un dérivation de la grammaire. L’arbre généré nous indique les différentes étapes de dérivation à appliquer à partir de l’axiome pour aboutir à la dérivation. Les schémas d’arbre réalisés dans le premier paragraphe sont des exemples d’arbres de dérivation. On distingue deux types d’analyse : les premières sont du type analyse descendante ou top-down et visent à parvenir à la séquence de terminaux visée depuis l’axiome. Les secondes sont du type analyse montante ou bottom-up et visent à parvenir à l’axiome en partant de la séquence de terminaux visée. Les analyses bottom-up sont intéressantes dans le sens où elles permettent plus facilement des analyses partielles que les top-down. C’est pourquoi dans des contextes peu rigoureux au niveau syntaxique, elles sont souvent préférées car elles renvoient toujours au moins un résultat partiel contrairement aux top-down qui ne peuvent qu’échouer dans la plupart des cas. Deux méthodes d’analyse servent de références dans le domaine des grammaires non contextuelles (type 2 et 3 de la hiérarchie) :
D’autres méthodes d’analyses existent également pour chacun des types de grammaire de la hiérarchie de Chomsky. Quelques exemples sont disponibles sur la page wikipédia consacrée à l’analyse syntaxique. PerspectivesJe réalise en ce moment une étude sur les parseurs syntaxiques existants en licence open source ayant atteint un niveau “état de l’art”. Je pense donc réaliser un billet ultérieurement sur ces parseurs et leurs performances. Mots clefs : analyse syntaxique, grammaire formelle, hiérarchie de Chomsky, TAL |
Merci beaucoup pour cet article, il m’a beaucoup aidé.
De rien. Merci à toi pour ton message.
[...] en matière d’analyse syntaxique où différentes écoles et formalismes se côtoient. Un autre billet de ce blog approche la syntaxe du point de vue de la grammaire formelle et des différents types [...]
Remember that this website is your shop where
you need to use Visual Merchandising with appropriate Seo tools.
A lower page rank represents a site that has little credibility according to Google.
All three applications offer full layer support, advanced filters and special effects, and included creative
content on top of basic photo editing tools.
The best way to encounter less risk with entrepreneurship and be more likely to succeed with your business is
to have a small initial investment, so you can begin making profit quicker.
For instance, if you type in “dentist” in the free Google Adwords tool you’ll find that dentists is the most widely used search consumers searching for a dentist type in. Most of the search engine optimization companies offer guaranteed services to the clients.
Everything said was actually very logical. However, consider this,
suppose you added a little content? I am not saying your
information is not solid, but what if you added a headline that grabbed a person’s attention? I mean Grammaires formelles et analyse syntaxique des langues | Blog Onyme is a little vanilla. You should look at Yahoo’s
home page and see how they create article headlines
to grab people interested. You might add a video or a picture or two to get
people excited about everything’ve written. Just my opinion, it would bring your website a little livelier.
These are the minimum requirements in order to run a Minecraft server.
Follow us on Facebook or Twitter for the latest news or
you can subscribe to our RSS feed or email alerts. Only a
small flavor games have as awesome a style to them as that one.
Wow that was unusual. I just wrote an incredibly long comment but after I clicked submit my comment didn’t show up.
Grrrr… well I’m not writing all that over again.
Regardless, just wanted to say superb blog!
Wonderful blog! I found it while surfing around on Yahoo News.
Do you have any suggestions on how to get listed in Yahoo News?
I’ve been trying for a while but I never seem to get there!
Thank you
I got this website from my buddy who told me concerning this site and at
the moment this time I am browsing this web site and reading
very informative articles or reviews here.
It is the traditionalist type address but nonetheless it is in tendency.
You can aquire an easy situation that will be not-too costly.
Just 9.56 inches higher and 7.47 inches wide,
the iPad is really small.
hOur company provides a wide variety of non prescription drugs. Look at our health website in case you want to strengthen your health with a help generic supplements. Our company offers herb-based healthcare products. Visit our health contributing portal in case you want to look better. Our company offers healthcare products. Take a look at our health contributing site in case you want to feel healthier. Our company provides a wide variety of non prescription drugs. Take a look at our health website in case you want to look healthier with a help health products. Our company offers herb-based weight loss products. Take a look at our health contributing portal in case you want to strengthen your health. Our company provides herbal pills. Visit our health contributing site in case you want to strengthen your health.
Our company provides supreme quality pills. Visit our health contributing website in case you want to improve your health. Our company provides herbal general health products. Take a look at our health contributing website in case you want to feel healthier. Our company provides non prescription products. Look at our health contributing website in case you want to strengthen your health. Our company offers a wide variety of non prescription products. Take a look at our health portal in case you want to look better with a help of health products. Our company offers supreme quality weight loss products. Look at our health contributing site in case you want to improve your health.