Blog Onyme
Sommaire
IntroductionOn entend assez souvent parler dans les domaines du TAL de méthodes statistiques pour analyser la sémantique des mots d’un texte. Ce billet est le premier d’une liste de billets visant à expliciter le lien existant entre les statistiques et la sémantique des mots en présentant quelques méthodes parmi les plus connues dans le domaine. Ce premier billet de la série est consacrée à la très célèbre méthode Latent Semantic Analysis (LSA).
Mais commençons d’abord par le commencement… Au croisement de la statistique et de la sémantique…C’est quoi une méthode statistique? C’est quoi le lien avec la sémantique? Entrons maintenant dans le vif du sujet avec la méthode du jour qu’est LSA…. Latent Semantic Analysis (LSA)Connaissances utiles pour implémenter la méthode :
Référence de la méthode : La méthode date de 1990 pour sa publication mais fut brevetée en 1988 aux États-Unis. Elle sert à quoi? Quelles sont les étapes principales?
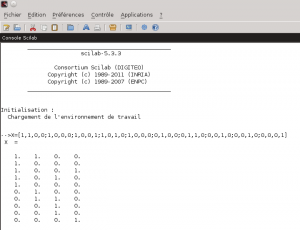
1- Construction de la matrice des occurrences X Voyons ce que cela peut donner sur un exemple très minimaliste. Prenons quatre documents : Il sont constitués de l’ensemble des mots suivants {Sarkozy, débute, campagne, présidentielle, UMP, affronte, Hollande, désigné, PS, tracteurs} après retrait de l’ensemble des mots creux {la, a, été, pour, il, y, des, en}. Nous pouvons alors représenter l’occurrence simple des termes dans les documents par la matrice X suivante :
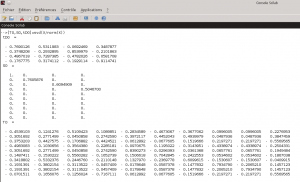
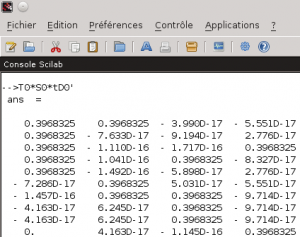
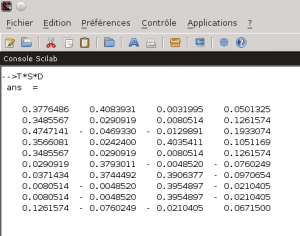
Nous allons utiliser un logiciel permettant de réaliser des calculs numériques. Vous connaissez peut être le logiciel MATLAB qui est assez réputé dans le domaine. Je vous propose cependant d’utiliser pour cet exemple un logiciel libre : Scilab Nous commençons donc par saisir la matrice X dans ce logiciel : 2- Décomposition de la matrice par des valeurs singulières Demandons à scilab de réaliser la décomposition en valeurs singulières (SVD) de notre matrice X normée : Attention! Scilab ne donne pas les matrices T0, S0 et tD0 telles que X/norm(X) = T0*S0*tD0 mais telles que X/norm(X) = T0*S0*tD0′ (tD0′ correspondant à la matrice transposée de tD0 et donc à D0) comme on peut facilement le vérifier… Nous avons donc quatre valeurs singulières pour notre exemple : 1 / 0.7605876 / 0.6094909 / 0.5046700 3- Réduction des matrices au rang k La réduction au rang k des matrices va permettre de se concentrer sur les plus fortes valeurs singulières. Si l’on considère la matrice X comme la matrice représentant les t×d liens existants entre les documents et les termes par l’intermédiaire d’un espace de concepts de taille m×m, cela revient à se concentrer uniquement sur les liens t×d existants entre les documents et les termes si l’on réduit l’espace de concepts à ses k dimensions les plus influentes sur l’espace des documents et des termes. Le gain espéré est dans les ressources nécessaires aux calculs puisque la réduction de l’espace intermédiaire aura comme conséquence une simplification des liens existants. En contrepartie, les finalités induites par les m-k dimensions abandonnées de l’espace intermédiaire seront perdues. L’astuce est donc dans le bon choix du rang k pour obtenir le meilleur rapport simplicité / pertinence. De plus, le passage par un espace intermédiaire de concepts permet à la méthode de prendre du recul sur les liens unissant les documents et les termes permettant par là l’apprentissage et l’exploitation de liens non triviaux de prime abord. Supposons que nous voulions faire une réduction au rang 3 de notre matrice X/norm(X) (et donc annuler la plus petite valeur singulière à savoir 0.5046700). Nous réduisons donc les rangs des matrices T0, S0 et D0 pour obtenir les matrices T, S et D à l’aide de Scilab : 4- Calcul de la matrice X^ Ce que Scilab peut nous faire facilement pour la matrice X^ de notre exemple : Et comment on l’utilise ce résultat? Traditionnellement, la distance du cosinus des vecteurs constituants les lignes de la matrice (dans le cas des termes) ou de ceux constituants les colonnes de la matrice (dans le cas des documents) est utilisée. Soit ti, le vecteur de la ième ligne (resp di, la ième colonne) de la matrice X^ représentative du ième terme (resp. document) et tj, le vecteur de la jème ligne (resp dj, la jème colonne) de la matrice X^ représentative du jème terme (resp. document). On a alors : De manière plus poussée, si l’on a une requête, on peut former un nouveau vecteur ri similaire à un vecteur di de la matrice X tel que les composantes de ce nouveau vecteur soit le centroid des termes de la requêtes. On a alors pour chaque document di du corpus d’origine : Bon me direz vous, et sur notre exemple qu’est ce que cela change concrétement? Un premier constat que l’on peut faire est que la matrice X^ est moins creuse que la matrice X (elle ne comporte plus aucune valeur nulle alors que la matrice originale en comporte 26 sur 40). Cette matrice semble donc dans un premier constat nous fournir des liens plus subtils entre les termes et les documents que la matrice originale. Intéressons nous particulièrement au dernier document. Celui-ci est ce que l’on pourrait considérer comme un intrus puisqu’il n’aborde pas la même thématique que les autres (à savoir la politique). Si l’on observe la matrice d’origine, l’exotérisme de ce document (la 4ème colonne de la matrice) n’est pas flagrant. Par contre, dans la matrice approchée X^, on constate que la dernière colonne contient des valeurs beaucoup plus faibles que les trois autres. En outre, la valeur la plus forte de cette colonne est 0.19 contre 0.47, 0.408 et 0.403 pour les trois autres. La méthode LSA en se concentrant sur les liens principaux entre les termes et les documents parvient à faire ressortir l’exotérisme du dernier document. La deuxième subtilité du corpus réside dans le piège linguistique du mot “campagne” évoqué dans ces deux principaux contextes sémantiques. La matrice originale X nous donne pour ce terme (3ème ligne de la matrice) une correspondance équivalente à 1 pour les documents 1 et 4 l’évoquant respectivement dans le contexte politique et dans celui de la ruralité. De ce fait, une requête menée sur ce corpus concernant le terme “campagne” ne pourrait pas faire le choix entre les deux contextes pourtant inégalitaire en terme de représentation (3 documents contre 1 en faveur de la politique). Il apparaît donc comme évident qu’une telle requête devrait privilégier le contexte dominant qu’est la politique. Là encore, la LSA parvient grâce à la transition par l’espace intermédiaire des concepts à privilégier le premier contexte au second. Ainsi, l’intersection entre le terme campagne et le document 1 (le sens politique du terme) est gratifié d’un 0.47 contre un 0.19 pour l’intersection avec le document 4 (le sens rural du terme). Cet exemple assez minimaliste mais comportant déjà des résultats intéressants montre l’intérêt de la méthode LSA dans le domaine assez vaste de la recherche d’informations et en particulier dans la fouille de texte (text mining) où elle permet d’indexer les textes non pas uniquement en fonction des mots qu’ils comportent mais en fonction de la sémantique latente qu’ils contiennent. Le mot de la finC’est fini pour aujourd’hui. Dans le prochain volet, nous parlerons de la méthode Hyperspace Analogue to Language (HAL). Mots clefs : décomposition de valeurs singulières, Latent Semantic Analysis, LSA, matrice de valeurs singulières, Scilab, sémantique, sémantique cachée, sémantique sous-jacente, sémantique statistique, SVD avec Scilab, TAL |

tres interesant
Merci
bonjour, merci pour votre article ! J’aimerais simplement vérifier : la matrice des valeurs singulières S0 est bien une m*n et non une m*m comme il est indiqué en 2 et en 3 ? C’est ce qu’on peut voir sur l’image matlab