Introduction

Un nouveau volet de notre saga de billets sur l’apprentissage artificiel. Dans celui-ci, nous allons discuter du moyen d’évaluer un apprentissage par l’estimation des risques.

• Apprentissage artificiel
• Fondements et protocoles pour la classification et les regroupements
• Moyens d’apprendre pour la classification et les regroupements (biais et modèles)
• Évaluation de l’apprentissage – Estimation des risques
• Évaluation de l’apprentissage – Précision / Rappel / F-mesure

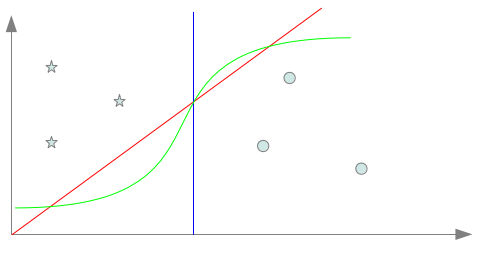
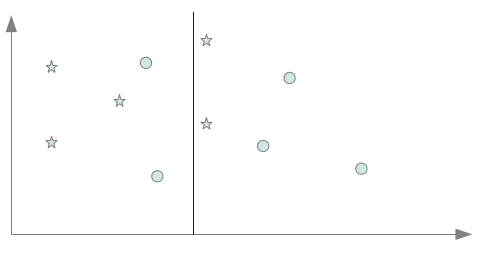
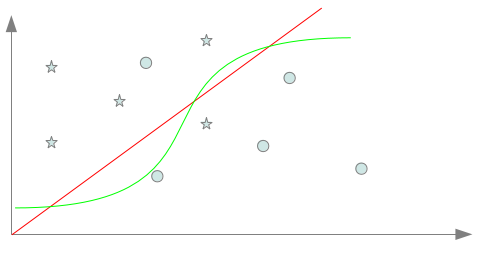
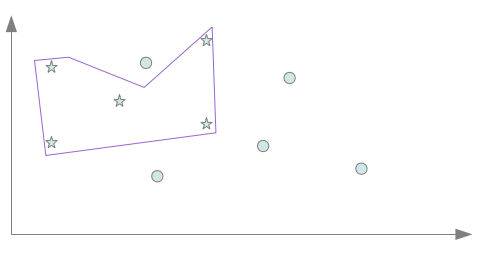
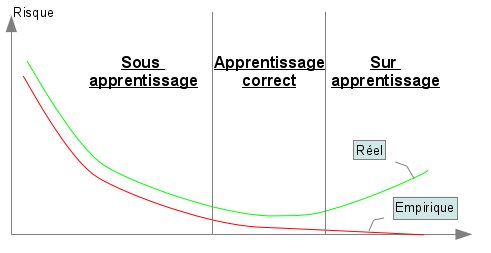
Nous voyons en quoi l’induction faite par le système apprenant peut conduire à une situation de mauvais apprentissage soit par une induction trop faible, soit au contraire par une induction trop forte.

D’un exemple pratique…

Nous allons commencer par un peu de pratique, ce qui va nous permettre d’introduire naturellement les deux pièges classiques de l’apprentissage. Reprenons l’exemple du billet précédent comportant six points classés dans deux classes distinctes.

Et nos trois séparateurs “acceptables” avec ces six instances

Comme nous l’avons évoqué dans le précédent billet, l’enjeu est de trouver un biais inductif capable à partir de quelques exemples de classer au mieux n’importe quel point et non pas seulement ceux connus lors de l’apprentissage. Pour illustrer cela, nous supposons que nous ayons à disposition après apprentissage deux points de plus pour chaque classe ce qui porte alors à 10 points (5 par classe), les points connus de l’espace après l’apprentissage.

Supposons que le biais inductif retenu pour l’apprentissage, nous fasse choisir le séparateur bleu. Celui-ci peut sembler un bon choix puisqu’il coupe l’espace en deux parties égales en séparant largement les 6 exemples connus selon leurs deux classes : en un mot, il semble donc réaliser une bonne induction. Nous obtenons alors, après apprentissage, la répartition décrite par la figure suivante :

On remarque assez rapidement que le classifieur commet dorénavant des erreurs et plus exactement deux erreurs par classes. cela amène alors à 4 points mal classés sur 10 : presque un point sur deux!!!! Ce classifieur qui pouvait paraître bon avec les 6 premiers exemples se révèle n’avoir pas choisi le bon biais inductif, du coup beaucoup des points non connus lors de l’apprentissage sont en fait mal classés par celui-ci. Nous sommes typiquement dans ce que l’on appelle une situation de sous apprentissage : les exemples connus lors de l’apprentissage n’ont pas permis d’avoir assez d’informations pour identifier un séparateur correct avec le biais inductif choisi.

Si l’on avait choisi un biais inductif nous amenant à choisir le séparateur rouge ou vert, nous aurions obtenu la répartition décrite par la figure suivante :

Il n’y a cette fois plus qu’un seul point par classe mal classé. Cela amène alors à seulement 2 points mal classés sur 10 : le biais inductif était donc cette fois meilleur!

Maintenant que l’on connait la classification de 10 points, nous pourrions être tenté d’apprendre à l’aide d’un nouveau biais inductif, un séparateur capable de classer convenablement l’ensemble des dix points à présent connus. Nous obtiendrions alors un séparateur proche de celui en mauve sur la figure ci-dessous.

Ce faisant, nous tombons à présent sur le deuxième piège de l’apprentissage : le séparateur mauve est clairement trop spécialisé sur les 10 points connus pour être un bon classifieur de l’ensemble des points de l’espace. Ce problème est largement connu en tant que situation de sur apprentissage.

Comme nous l’avons vu au travers de cet exemple, les deux pièges de l’apprentissage ne sont pas décorrélés. En cherchant à s’éloigner du premier, nous sommes tombé sur le deuxième et inversement en cherchant à éviter le deuxième (en prenant le séparateur bleu), nous nous sommes confrontés au premier.

Il nous faut trouver un compromis se situant entre le séparateur trop inductif nous conduisant à une situation de sous apprentissage et celui trop spécifique nous conduisant en sur apprentissage.

… à la définition des risques

Formellement, nous recherchons une fonction h permettant de classer les données x de X selon des classes y de Y tel que :

Nous notons y’, la classe de Y correspondant à l’étiquetage idéal d’une donnée x de X. La fonction h* idéale recherchée doit donc classer toutes les données de X selon :

La recherche du compromis mentionné auparavant correspond à une recherche du séparateur engendrant un risque minimale de mauvaise classification. Ce risque de mauvaise classification, appelée risque réel est donné par :

La fonction l(y,y’) donne le coût de perte entre l’étiquetage y et y’. Cela correspond à la “sanction” que l’on doit considérer pour l’étiquetage d’une donnée par y au lieu de y’. Cela est notamment utile si des étiquetages doivent être considérés comme pire que d’autres. Pxy’ correspond à la probabilité qu’une donnée x à étiqueter par y’ apparaisse en tant que donnée à classer. La fonction de perte l est dépendante de la tâche à accomplir. Cela peut être classiquement une fonction binaire accordant une sanction de 0 en cas de correspondance et une sanction de 1 en cas de divergence. Cela peut aussi être une fonction plus complexe…

Calculer le risque réel suppose donc de connaître tous les points de l’espace d’entrée, leur étiquetage idéal et leur probabilité d’apparition en tant que donnée à classer : une supposition illusoire! Nous devons donc nous contenter d’une approximation de ce risque. Une technique courante est d’utiliser le risque empirique calculé à partir des exemples d’apprentissage. Notons L, l’ensemble des exemples d’apprentissage disponibles.

Le risque empirique permet d’obtenir une approximation imparfaite du risque réel. Le risque empirique peut être diminué en effectuant un sur apprentissage qui augmente lui le risque réel. Cette situation n’étant pas souhaitable, il convient de choisir un biais suffisamment fort pour empêcher le sur apprentissage. La figure ci dessous montre l’évolution simultanée des deux risques et les deux situations de mauvais apprentissage que nous avons évoquées dans la partie précédente.

Conclusion

Nous avons vu les notions de risques et surtout la notion de fonction de perte l qui permet de les obtenir. Cette notion de fonction de perte est pour le moment assez abstraite. Dans le prochain volet, nous voyons comment les techniques d’évaluations utilisées en recherche d’informations (précision, rappel, F-mesure) peuvent être employées pour évaluer concrètement un apprentissage.

Mots clefs : apprentissage artificiel, apprentissage automatique, apprentissage supervisé, classification, principe de minimisation du risque empirique, risque empirique, risque réel, sous apprentissage, sur apprentissage, TAL

Cette entrée a été publiée le Jeudi 30 août 2012 à 10 h 11 min, et rangée dans Apprentissages, TAL. Vous pouvez suivre les réponses à cette entrée via son flux RSS 2.0. Vous pouvez laisser un commentaire, ou faire un rétrolien depuis votre site.